算法作业-有向图

发表于 | 更新于 | 分类于

算法作业

​ 近期算法布置了一篇课设，在这里描述一下，并晒一下代码。整体来说算法实验很简单，实现方法也很简单粗暴，不过练习一下图的写法吧。

(PS.博主使用的是eclipse for C++，可以利用debug纠错)

问题描述

  1. 生成100个点，500条边的有向图，任选一点为源点，计算s到其它点的距离。（用邻接链表存储）
  2. 将上述有向图变成dag图，从中去掉一些边，不允许使用递归
  3. 计算上述dag图中最长路径，并记录下路径

问题一

生成100个点，500条边的有向图，任选一点为源点，计算s到其它点的距离。（用邻接链表存储）

问题分析

因为需要用邻接链表存储，因此需要用一个链表结构，基本结构如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
struct node{
public:
	node* next=NULL;//下一个
	int weight=-1;
	int ini=0;//入度
	int id=-1;//本node的编号
public:
	void init(node* next,int length,int id){//初始化方法
		this->next=next;
		this->weight=length;
	}
	void init(int length,int id){//初始化方法
		weight=length;
		this->id=id;
	}
	void init(int id){//初始化方法
		this->id=id;
	}
	bool existedge(int i){//查看是否此边已存在。
		node* current=this;
		if(i==id){
			return true;
		}//自环
		while(current->next!=NULL){
			if(current->next->id==i){
				return true;
			}
			current=current->next;
		}
		return false;
	}

};

这里，我写的node的性质比较多，但是事实上是完全没有必要的，如我的小伙伴就只存了一个id，后来证明她这种做法更为合理。

下面需要考虑建一个图需要什么样的方法，由于博主之前写过后缀树一类的，因此这个还是很easy的，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Arithmex1 {
public:
	Arithmex1(int , int );
	virtual ~Arithmex1();

		int n=0;//顶点数
		int e=0;//边数
		int time=0;
		bool create() ;//创建图，是否存在边
		bool insertEdge(int,int);
			//插入边

		bool eraseEdge(int,int);//删除边
		int weight(int,int);//某一边的权重
		int distance(int);//任选一点为源点，计算s到其它点的距离
		void dfs(int);
		int maxdis();//计算dag图中最长路径，并记录下路径
		void dag();//将图变成dag图
//		其他方法
		bool directed();
		void print();//图的打印
};

下面开始图的主要代码：

create方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool Arithmex1::create(){
		srand(10);//设置随机数种子
		graph=new node[n];//是一个装了node（首）的数组
		for(int i=0;i<n;i++){
			graph[i].init(1,i+1);//于是附上初值，权重为1，编号为i+1;
		}
		int j=0;
		while(j<e){
			int tmp1=rand()%n+1;//对应ID
			int tmp2=rand()%n+1;//dui
			if(!graph[tmp1-1].existedge(tmp2)){
				insertEdge(tmp1,tmp2);
			}else{
				continue;
			}
			j++;
		}
}

insertEdge方法(简单的，链表插入的方法)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool Arithmex1::insertEdge(int a,int b){//插入边
	if(!graph[a-1].existedge(b)){
		node* current=&graph[a-1];
		while(current->next!=NULL){
			current=current->next;
		}
		node *newnode=new node();
		newnode->init(1,b);
		current->next=newnode;
		graph[b-1].ini++;
		return true;

	}
	return false;
}

博主为了方便，写的方法比较粗暴，因此只是作为参考。值得注意的是，当我们以node来表示节点时，节点在存储空间内不止有一个。如下图：数组中有一个1，链表中2/4后也均有1，因此就像上面说的，在node struct中增加属性没有必要，且可能浪费空间，这时候一个好的做法是维护一个同等规模的数组来保存节点的属性

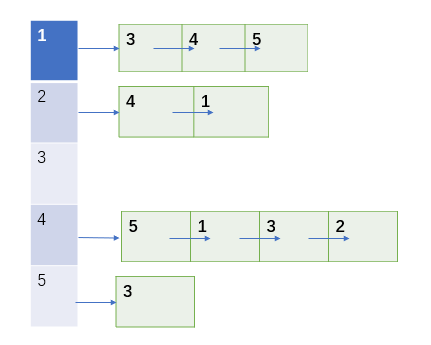
desc1

下面是需要计算源点s到图中各点的距离，显然可以用BFS,主要思路是维持一个数组存储长度，子节点的长度是父节点长度+1；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int Arithmex1::distance(int i){
	int source=i;
	node* current=&graph[source-1];//得到源点位置
	int tip[n];//tip，标记源点
	for(int j=0;j<n;j++){//标记，有没有被找到过
		tip[j]=0;
	}
	int tis[n];//tip，标记源点
	for(int j=0;j<n;j++){//距离，有多远
		tis[j]=-1;//开始认为不可达
	}
	tip[source-1]=-1;//设为首节点认为已标记
	tis[source-1]=0;//距源点为0
	queue<node*> tmp;
	tmp.push(current);//头结点

	while(!tmp.empty()){
		node* tt=tmp.front();//头结点
		tt=&graph[tt->id-1];//找到在链表中的位置
		tmp.pop();
		node* cnode=tt;
		while(cnode->next!=NULL){//遍历其邻接链表
			if(tip[cnode->next->id-1]!=-1){//如果没有做过标记
				tmp.push(cnode->next);//推入队列
				tis[cnode->next->id-1]=tis[tt->id-1]+1;
				tip[cnode->next->id-1]=-1;//同时做上标记，已扫描
//				cout<<cnode->next->id<<" "<<tis[cnode->next->id-1]<<" ]]";

			}
			cnode=cnode->next;//去下一个
		}
	}
	for(int i=0;i<n;i++){
		cout<<graph[i].id<<"的距离是==>  "<<tis[i];
		cout<<endl;
	}


}

问题二

将上述有向图变成dag图，从中去掉一些边，不允许使用递归

问题分析

这里的一个简单思路就是删除返回边。根据《算法导论》上的算法描述，即dfs时遇到灰色节点，边可被删除。难点主要在于白色、黑色、灰色（也可以是开始时间、结束时间）的判定。另一个难点在于不允许使用递归。这里面有很多种情况，需要仔细判定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
void Arithmex1::dfs(int start){
	//链表属性
	node* current=&graph[start-1];//得到源点位置
	stack<int> ppid;//记录压入栈时的先驱点
	stack<node*> dfss;//记录压入栈的node，有一个固定的id，只需要用id与遍历
	ppid.push(-1);//起始点先驱点为-1
	dfss.push(current);//放入当前点
	while(!dfss.empty()){
		node* newnode=dfss.top();//得到node
//		cout<<"新一轮循环"<<newnode->id<<endl;
		dfss.pop();
		int tpid=ppid.top();//当前点newnode押出栈时的先驱点
		ppid.pop();//当前节点先驱点
		if(pro[newnode->id-1].color==0){//如果其颜色=0
			pro[newnode->id-1].color =1;//pop出，正式找其它点，变灰色
			pro[newnode->id-1].distime=++time;//发现时间
			node* current=&graph[newnode->id-1];//找到图中它的位置就可以遍历链表

			int num=0;//是否变黑，只要push进去节点，说明都没有完成，完成的才变黑

			while(current!=NULL&&current->next!=NULL){//遍历其邻接链表

				if(pro[current->next->id-1].color ==0){//如果没有做过标记

					pro[current->next->id-1].pid=newnode->id;//随时会变会更新的pid
					dfss.push(current->next);//压入栈
					ppid.push(newnode->id);//这个对应的pid
//					cout<<"放入"<<current->next->id<<endl;
					num++;//操作未完成
				}else if(pro[current->next->id-1].color==1){//如果找到了灰色的，返回边。

//					cout<<current->id<<"shiyan"<<endl;
//					cout<<current->next->id<<"shiyan"<<endl;
					change=eraseEdge(newnode->id,current->next->id);//删除
//					print();
				}
				if(!change){

					current=current->next;
				}else{
					change=false;
				}

			}


			if(num==0){//叶子节点或者无用节点，本节点可以为0
				pro[newnode->id-1].color=2;//黑色
				pro[newnode->id-1].fintime=++time;
				//开始追根溯源


				int tmpid=pro[newnode->id-1].pid;
				if(!ppid.empty()){

					while(tmpid!=ppid.top()){

						pro[tmpid-1].color=2;
						pro[tmpid-1].fintime=++time;
						tmpid=pro[tmpid-1].pid;
					}
				}else{
					pro[tmpid-1].color=2;
					pro[tmpid-1].fintime=++time;
	//				tmpid=pro[tmpid-1].pid;
				}
			}
		}else if(pro[newnode->id-1].color==2){//早之前已经发现

			int tmpid=tpid;
			if(!ppid.empty()){
				while(tmpid!=ppid.top()){
//					cout<<tmpid<<"pout"<<endl;
					pro[tmpid-1].color=2;
					pro[tmpid-1].fintime=++time;
					tmpid=pro[tmpid-1].pid;
				}
			}else{
				pro[tmpid-1].color=2;
				pro[tmpid-1].fintime=++time;

			}
		}

	}
}

因为有的节点入度=0，即一次dfs会忽视它们，因此可以采用直接遍历的方法

1
2
3
4
5
6
7
void Arithmex1::dag(){
	for(int i=0;i<n;i++){
		if(pro[i].color==0)
			dfs(i+1);
	}
	print();
}

问题三

计算上述dag图中最长路径，并记录下路径。

问题分析

看到这个题，第一感觉是用拓扑序列，因为拓扑头一定是头结点。

但是博主又想偷懒了，拓扑头怎么求？在上文中，我们已经求出了结束时间最晚的那个节点，无疑一定是拓扑头。但是这里，博主直接采用的入度为0的为拓扑头，（再维持一个数组添加入度属性啦，插入边入度+1，删除边入度-1），这里，只要从拓扑头开始bfs（注意，这里让求的是最长路径，因此无需判断bfs时此点有没有访问过，而且是有向无环图，所以不会死循环）

这是一种比较简单的思路，却需要大量空间时间，另一种比较好的方法是完全用拓扑序列来实现。至于一些细节就不再赘述，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
int Arithmex1::maxdis(){
	int* maxpid;
	maxpid=new int[n];
	for(int j=0;j<n;j++){//距离长短
					maxpid[j]=-1;
				}
	int* tmppid;
	tmppid=new int[n];
	for(int j=0;j<n;j++){//距离长短
					tmppid[j]=-1;
				}
	int lastid=0;
	int realastid=-1;
	int maxdis=0;
	int cc=0;
	for(int i=0;i<n;i++){//遍历顶点
//		cout<<graph[i].ini<<endl;
		if((graph[i].ini==0)){//入度==0
			cc++;
			int tis[n];//tip，标记源点
			for(int j=0;j<n;j++){//距离长短
				tis[j]=-1;
			}
			tis[i]=0;//到自己的距离为0
			int tmpdis=0;
//			tis[i]=1;
			node* current=&graph[i];//得到源点位置
			queue<node*> tmp;
			tmp.push(current);//头结点

			while(!tmp.empty()){
				node* tt=tmp.front();//头结点
				tt=&graph[tt->id-1];//找到在链表中的位置
				tmp.pop();
				node* cnode=tt;

				while(cnode->next!=NULL){//遍历其邻接链表
					tmp.push(cnode->next);//推入队列
					tis[cnode->next->id-1]=tis[tt->id-1]+1;
					tmpdis=tis[cnode->next->id-1];
					lastid=cnode->next->id;
					tmppid[cnode->next->id-1]=tt->id;
					cnode=cnode->next;//去下一个
				}
				if(cnode->next==NULL){
					lastid=cnode->id;
				}

			}


			if(maxdis<tmpdis){
				realastid=lastid;
				maxdis=tmpdis;
				maxpid=tmppid;
				for(int j=0;j<n;j++){//距离长短
					maxpid[j]=tmppid[j];
//					cout<<tmppid[j]<<"||"<<maxpid[j]<<" ";
				}
				cout<<endl;
				tmppid=new int[n];
				for(int j=0;j<n;j++){//距离长短
					tmppid[j]=-1;
				}
			}
		}

	}
	tmppid=new int[maxdis+1];
	for(int j=0;j<maxdis+1;j++){//距离长短
		tmppid[j]=-1;
	}
	if(realastid!=-1)lastid=realastid;
	int jianyan=lastid;
	tmppid[maxdis]=lastid;
	int count=maxdis-1;

	while(jianyan!=-1){
		jianyan=maxpid[jianyan-1];
		tmppid[count]=jianyan;
		count--;
	}
	cout<<endl;
	for(int j=0;j<maxdis+1;j++){//距离长短
		cout<<tmppid[j]<<" ";
	}
	cout<<endl;
	return maxdis;
}

更多完整代码参见https://github.com/yongbosmart