半边数据结构&网格细分
参考博客:
https://blog.csdn.net/lafengxiaoyu/article/details/51524361
https://blog.csdn.net/outtt/article/details/78544053
http://www.cnblogs.com/shushen/p/5251070.html
对于表面网络来说,其重要的特点在于拓扑,也就是曲面是如何表达的,而不是其顶点的位置。拓扑的不同造就了不同的数据结构和标准,不同的拓扑,其进行网格查询和编辑的性能也不同。
计算机图形学上,通常说的流形是一种几何模型表面(但不是所有的),即二维流形,对应拓扑流形。如果网格的每个边最多被两个面片共用,那么这个网格就是流形网络,否则称为非流形网络。
半边数据结构:
最大特点是半边,每个边分为两个半边,每个半边都是一个有向边,方向相反。如果一个边被两个面片公用,则每个面片都能各自拥有一个半边。如果一个边仅被一个面片占用(边界边),则这个面片仅拥有该边的其中一个半边,另一个半边为闲置状态。每一条半边仅存储它的起点指针
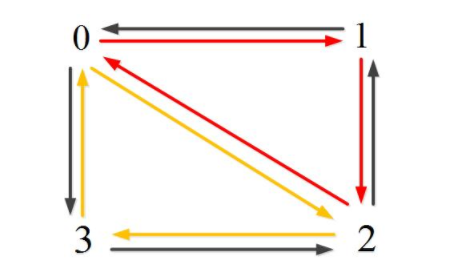
半边数据结构仅支持流形网络。
半边数据结构的三个重要的数据结构——顶点、半边、面片
- 顶点(Vertex):包含出半边(OutgoingHalfedge)的指针或索引
在半边数据结构中的点储存着x,y,z的位置和以其为起始点的半边的指针。在任意给定的点上存在超过一条我们可以选择的半边,但是我们只需要选择其中一条并且是哪一条没关系,在下面的查询方法中我们会看到解释。
1 | struct HE_vert |
- 半边(HalfEdge):包含终点(StartVertex)、邻接面(AdjacentFace)、下一条半边(NextHalfedge)、相反边(opposite)的指针或索引
1 | struct HE_edge |
- 面片(Face):包含一条起始边(FirstHalfedge)的指针或索引对于一个半边数据结构的简单形式,一个面仅仅需要储存一个围绕它的边的指针,在一些特定场合可能要求我们储存比如材质和法向一类的信息。和上面一样,虽然有很多边围绕着面,我们只需要储存其中一条,而无所谓是哪一条
1 | struct HE_face |
现在问题来了。顶点可能有两条或以上的出半边,而顶点的数据表达只有一条出半边,那这条出半边是哪一条?半边的下一条半边又是哪一条?面片的起始半边又是哪一条?通过某个网格的数据结构图(如图1)能看得出这些信息吗?
答:事实上,半边数据结构的网格的构建通常是通过面列表来创建的,也就是说,正常的构建半边数据结构网格是通过一个一个面片的添加来构建的。
所以面的添加顺序就决定了点边面结构的信息,添加面的方法通常是addFace(a,b,c,…),a,b,c…参数是该面片按其某条环路顺序排列的顶点的指针或索引。注意,环路可以是顺时针或者逆时针,决定了该面片的方向(法向量的方向)。
三维网格细分算法:
Catmull-Clark subdivision
Catmull-Clark细分是一种四边形网格的细分法则,每个面计算生成一个新的顶点,每条边计算生成一个新的顶点,同时每个原始顶点更新位置。
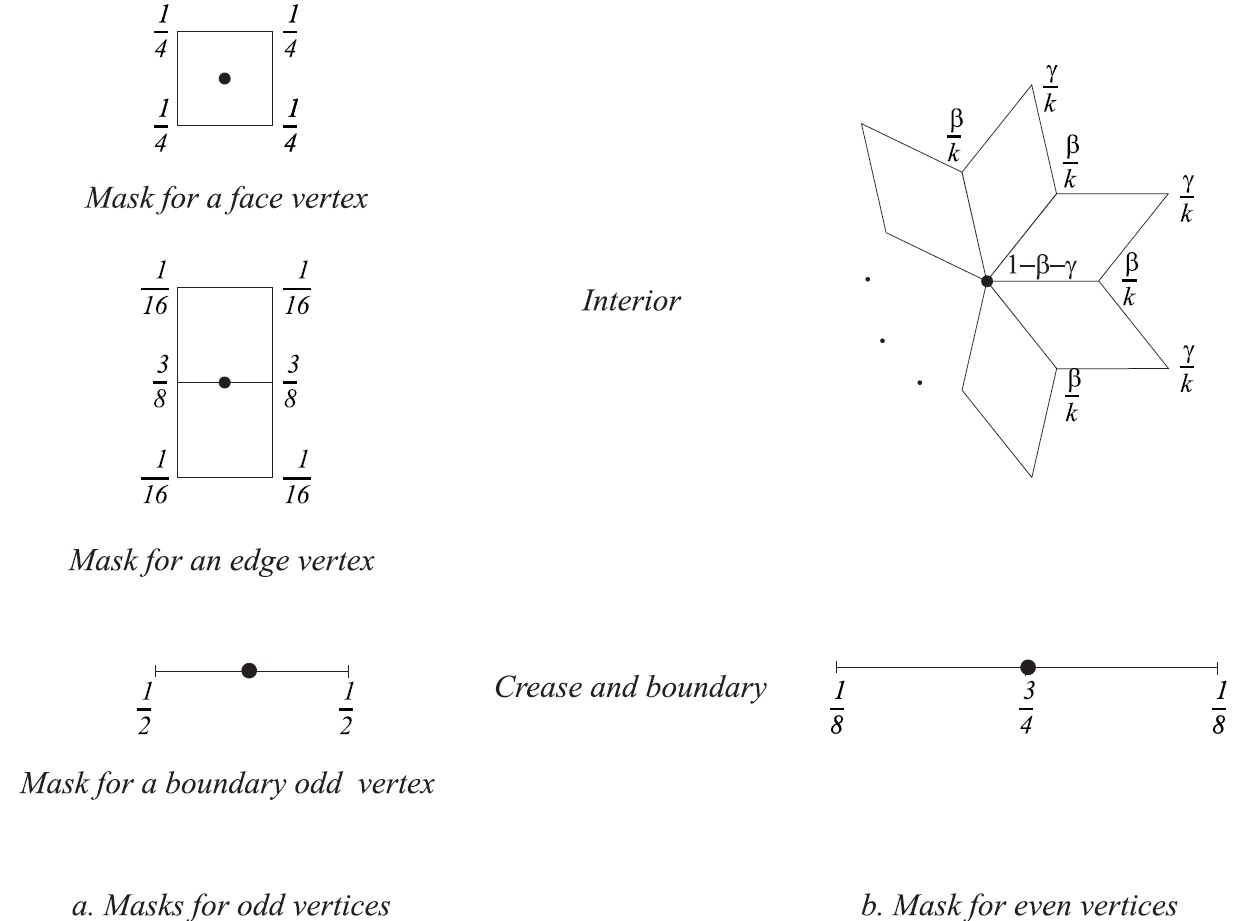
1.网格内部F-顶点位置:
设四边形的四个顶点为v0、v1、v2、v3,则新增加的顶点位置为v = $\frac{1}{4}$ ×(v0 + v1 + v2 + v3)。
2.网格内部V-顶点位置:
设内部顶点v0的相邻点为v1、v2,…,v2n,则该顶点更新后位置为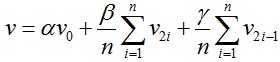 ,其中α、β、γ分别为α = 1 - β - γ。
,其中α、β、γ分别为α = 1 - β - γ。
3.网格边界V-顶点位置:
设边界顶点v0的两个相邻点为v1、v2,则该顶点更新后位置为v = $\frac{3}{4}\frac{1}{8}$×(v1 + v2)。
4.网格内部E-顶点位置:
设内部边的两个端点为v0、v1,与该边相邻的两个四边形顶点分别为v0、v1、v2、v3和v0、v1、v4、v5,则新增加的顶点位置为v = $\frac{1}{4}$ (v0 + v1 + vf1 + vf2) = $\frac{3}{8}$ (v0 + v1) + $\frac{1}{16}$ (v2 + v3 + v4 + v5)。
5.网格边界E-顶点位置:
设边界边的两个端点为v0、v1,则新增加的顶点位置为v = $\frac{1}{2}$ (v0 + v1)。
Loop subdivision
Loop细分是一种三角形网格的细分法则,它按照1-4三角形分裂,每条边计算生成一个新的顶点,同时每个原始顶点更新位置。下图为Loop细分格式的细分掩膜,对于新增加的顶点位置以及原始顶点位置更新规则如下:
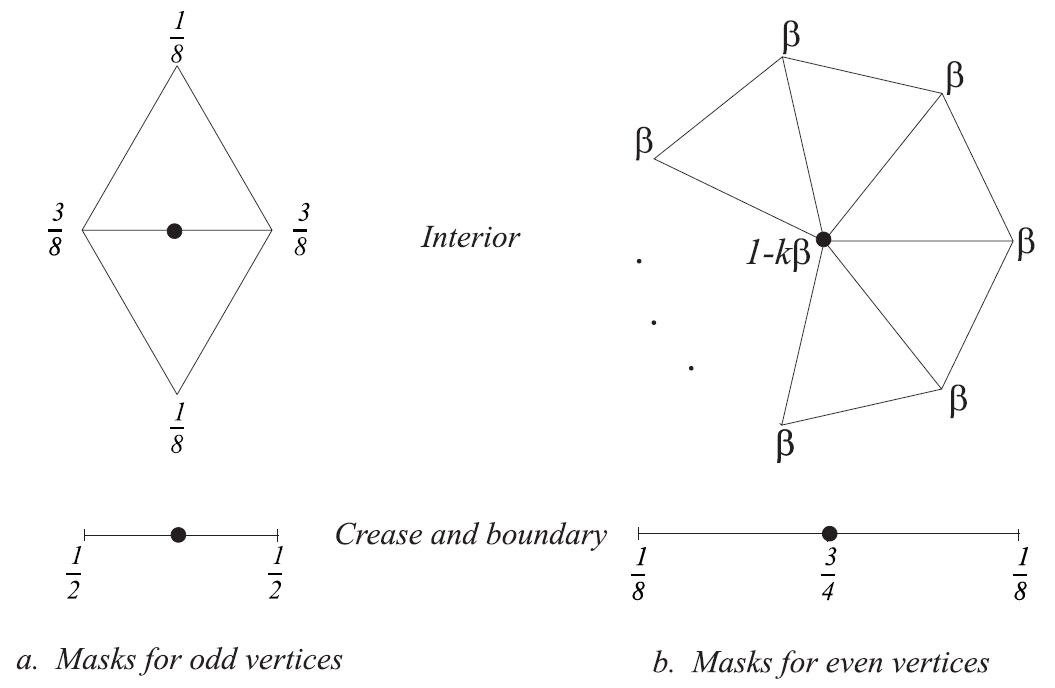
1.网格内部V-顶点位置:
设内部顶点v0的相邻点为v1、v2,…,vn,则该顶点更新后位置为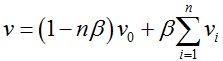 ,其中
,其中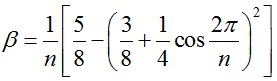 。
。
2.网格边界V-顶点位置:
设边界顶点v0的两个相邻点为v1、v2,则该顶点更新后位置为 v = $\frac{3}{4}$ ×v0 + $\frac{1}{8}$ ×(v1 + v2)。。
3.网格内部E-顶点位置(新增点):
设内部边的两个端点为v0、v1,相对的两个顶点为v2、v3,则新增加的顶点位置为v = $\frac{3}{8}$ (v0 + v1) + $\frac{1}{8}$(v2 + v3)。
网格内部某条边的两个端点为v0、v1,共享这条边的两个三角形的面是(v0,v1,v2)和(v0,v1,v3)
4.网格边界E-顶点位置(新增点):
设边界边的两个端点为v0、v1,则新增加的顶点位置为v = $\frac{1}{2}$×(v0 + v1)。