KNN算法

发表于 | 更新于 | 分类于

KNN算法

概述

KNN算法，即K近邻算法，是一个有标签的分类算法。（不同于K-means，是一个无标签的聚类算法）

KNN的思想可以简单描述为，将测试数据映射到样本空间，测试数据周围是什么类别的居多，则测试数据本身可认为是什么类别的。这里的K代表的是依据测试数据周围最近的样本的数目。

比如常见的一个例子，如下图（图源于网络）

举例

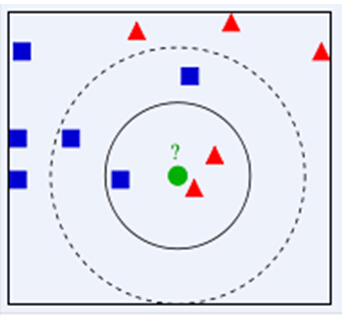
k=3时，观察绿色周围最近的3个图案，则绿色图形归于红色一类。

k=5时，观察绿色周围最近的5个图案，则绿色图形归于蓝色一类。

具体阐释

定义

它的工作原理是：存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的
特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。

一般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法中k的出处，通常k是不大于20的整数。

最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

主要流程

K近邻主要是将测试数据与已知标签数据进行相似性比较，因此需要对数据进行规范化处理，以便比较。

关于特征空间距离的度量（两向量相似度的测量）有多种方式。常用的有欧式距离、曼哈顿距离等。

（以下代码来自《机器学习实战》，采用欧氏距离)

欧式距离公式 向量A、B的距离为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#inX - 用于要进行分类判别的数据(来自测试集) dataSet - 用于训练的数据(训练集)
#labes - 分类标签 k - kNN算法参数,选择距离最小的k个点
def classify0(inX,dataSet,labels,k):
    m=dataSet.shape[0] #返回dataset的行数，即已知数据集中所有点的数量
    diffMat=np.tile(inX,(m,1))-dataSet #行向量方向上将inX复制m次
    sqDiffMat=diffMat**2 #减完后，对每个数做平方
    sqDistances=sqDiffMat.sum(axis=1) #平方后按行求和
    distances=sqDistances**0.5 #开方算出欧式距离
    sortedDistIndicies=distances.argsort()#对距离从小到大排序，并把索引输出
    classCount={} #用于类别/次数的字典，key为类别，value为次数
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)

    # 把计数最大的值所对应的标签返回出去
    return sortedClassCount[0][0]

也可以使用sklearn实现，比较方便。

k值的选择

k值的选择会对k近邻法的结果产生重大影响。

如果选择较小的k值，就相当于用较小的邻域中的训练实例进行预测，“学习”的近似误差（approximation error）会减小，只有与输入实例较近的（相似的）训练实例才会对预测结果起作用。但缺点是学习误差会增大。如果近邻点刚好是噪声，预测就会出错。换句话说，容易产生过拟合现象。

如果选择较大的k值，就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大。这时与输入实例较远的不太相似的实例也会起预测作用，使预测出错。

优缺点

优点：精度高、对异常值不敏感、无数据输入假定。
缺点：计算复杂度高、空间复杂度高。
适用数据范围：数值型和标称型。

参考资料

[1] P. 哈林顿 (Harrington and 李锐, 机器学习实战. 2013.

[2] 李航, 统计学习方法. 2012.